Numeri positivi e negativi (Rappresentazione in modulo e segno)
Aggiungiamo un bit che è pari a
- 0 per il segno +
- 1 per il segno –
Il vantaggio è che il segno può essere staccato e si può ricavare il modulo. Rappresentiamo solo 128 numeri positivi e 127 (+ il -0) numeri negativi
Complemento a 2
La prima cifra ha sempre un segno negativo. Se la prima cifra è 0, il numero sarà positivo, se la prima cifra è 1 il numero sarà negativo.
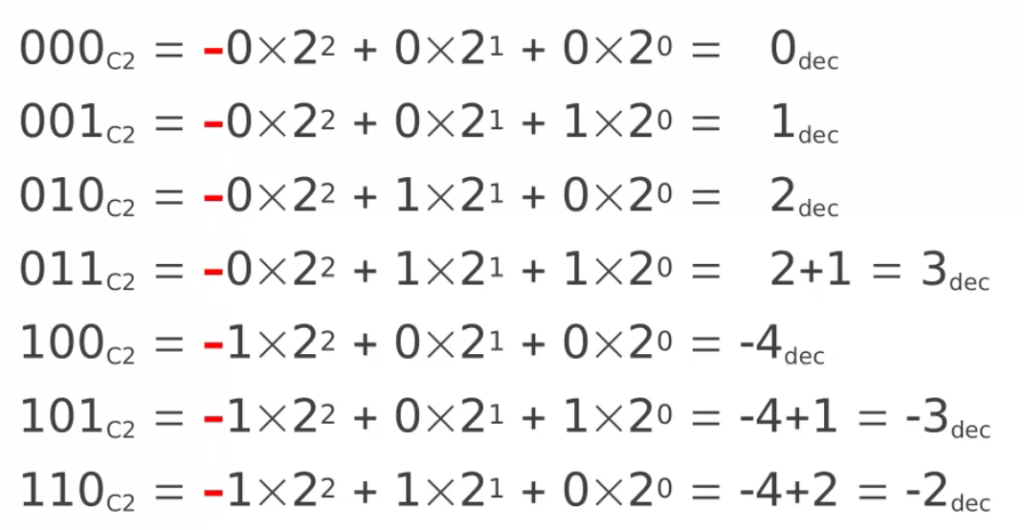
Qualora si volesse rappresentare il +7 nella codifica complemento a 2, invece di scrivere 111, scriveremo 0111. (nella rappresentazione in modulo e segno). Se invece vogliamo indicare solo il modulo, esso sarà sempre 7.
Invertire un numero in Complemento a 2
- Dobbiamo invertire ogni bit del numero
- Sommiamo 1 alla posizione meno significativa
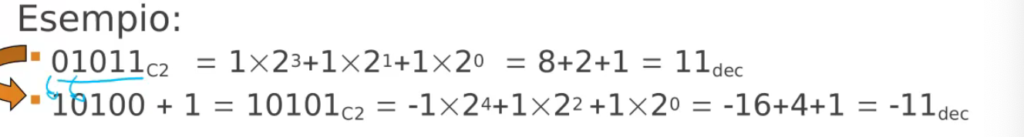
Conversione dec → C2
Prima si converte in binario e poi si mette lo 0 davanti al numero.
Es. 154 dec → 10011010 bin → 010011010 C2
Conversione da decimale negativo a complemento a 2

Somma in complemento a 2
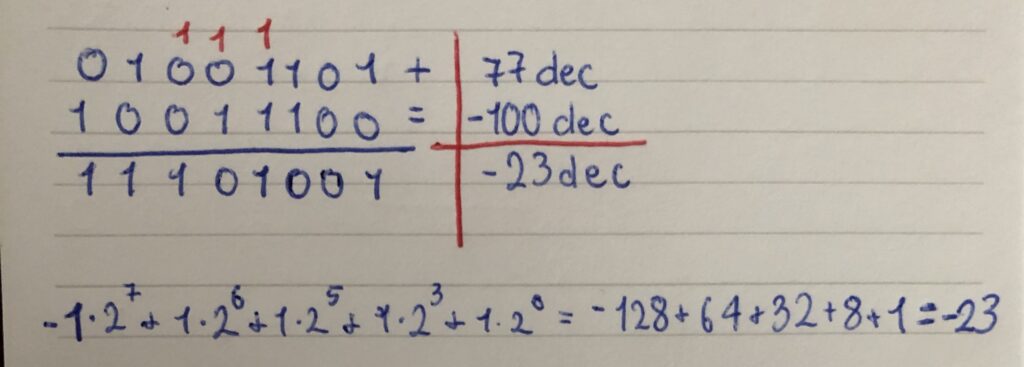
⁉️ Anche qui esiste l’overflow → anche se non si perde il riporto. Dovremmo aggiungere un bit. (esempio: 77 + 92 = -87) in Complemento a 2. Ce ne accorgiamo perchè se il primo numero da sinistra è 1, vuol dire che il numero è negativo.
Si ha overflow quando il risultato corretto eccede il potere di rappresentazione dei bit a disposizione. Si può avere overflow con riporto perduto e si può avere un riporto perduto senza **overflow: (**esempio: 12 – 7 in complemento a 2).
L’overflow si può rilevare:
- Se gli addendi sono discordi non si verifica mai
- Se gli addendi sono concordi tra loro, si verifica se il risultato è discorde.

